感知机

1. 概述

感知机是一种用于二分类的线性分类模型，输入为实例的特征向量，输出为实例的类别，取$+1$和$-1$二值。感知机对应于输入空间中将实例划分为正负两类的分离超平面，属于判别模型。感知机的目的是训练出将输入数据进行二分类的超平面；因此，可以导入基于误分类的损失函数，并利用梯度下降算法对损失函数进行极小化，以此得到感知机模型。

2. 感知机(简洁版)

2.1模型

定义由输入空间到输出空间的函数：

$$f(x)=sign(wx+b)$$

称感知机。其中，权重$w$和偏置$b$是感知机的参数，$sign$是符号函数。感知机是一种线性分类模型，属于判别模型。

由上可知，对于感知机，输出值无非不过两种情况：

$$wx+b>0/wx+b<0$$

而我们要找的超平面为

$$wx+b=0$$

注意，数据集必须要线性可分。

2.2学习策略

a)损失函数

$$-\frac{1}{|w|}\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$$

是所有误分类点到超平面$S$的总距离，其中

$$-\frac{1}{|w|}$$

为$w$的$L_2$范数，若不考虑，则损失函数的定义为：

$$L(w,b)=-\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$$

这是关于$w$,$b$的连续可导函数。

b)学习算法

获得感知机模型的过程本质上就是极小化损失函数的过程：

$$\underset{w,b}{min}L(w,b)=-\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$$

假设误分类点集合是固定的，那么损失函数$L(w,b)$的梯度由：
$${\mathrm{\nabla }}_{w}L(w,b)=-\sum _{x_i\in M}{y}_i{x}_i$$

$${\mathrm{\nabla }}_{b}L(w,b)=-\sum _{x_i\in M}{y}_i$$
给出。

随机选取一个误分类点$(x_i,y_i)$，对$w$,$b$进行更新：

$$w\leftarrow w+\eta y_i{x}_i$$

$$b\leftarrow b+\eta y_i$$
其中$\eta$是学习率。

3. 实现代码

#!/usr/bin/env python
# -*- encoding: utf-8 -*-
'''
@File    :   感知机.ipynb
@Time    :   2025/03/24 21:29:44
@Author  :   Neutrin 
'''

# here put the import lib
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)  

# 生成样本点 100个负样本 100个正样本
n_samples_neg = 100
X_neg = np.random.normal(loc=[-2, -2], scale=1.0, size=(n_samples_neg, 2))
y_neg = np.zeros(n_samples_neg)

n_samples_pos = 100
X_pos = np.random.normal(loc=[2, 2], scale=1.0, size=(n_samples_pos, 2))
y_pos = np.ones(n_samples_pos)

# 合并样本点
X = np.vstack((X_neg, X_pos))
y = np.hstack((y_neg, y_pos))

# 可视化
plt.figure(figsize=(8, 6))
plt.scatter(X_neg[:, 0], X_neg[:, 1], c='blue', marker='o', label='Class 0')
plt.scatter(X_pos[:, 0], X_pos[:, 1], c='red', marker='x', label='Class 1')
plt.title('Perceptron Training Data')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.grid(True)
plt.show()

print(f"Dataset shape: X: {X.shape}, y: {y.shape}")
# 感知机用于二分类问题，输出为+1或-1
def out(x, w, b):
    return np.sign(np.dot(x, w) + b)

class Perceptron: 
    def __init__(self, learning_rate=0.01, max_iterations=1000):  # 学习率和最大迭代次数
        self.learning_rate = learning_rate
        self.max_iterations = max_iterations
        self.w = None
        self.b = None
    
    def fit(self, X, y):
        # 初始化权重和偏置
        n_samples, n_features = X.shape  # 样本数和特征数
        self.w = np.zeros(n_features)
        self.b = 0
        
        # 将标签0转为-1 (感知机标签通常为-1和+1)
        y_transformed = np.where(y == 0, -1, 1) # where函数，满足条件输出1，不满足输出0
        
        # 训练模型
        for _ in range(self.max_iterations):
            misclassified = 0               # 错误分类的样本数
            for idx, x_i in enumerate(X):   
                y_i = y_transformed[idx]
                # 如果预测错误，更新权重
                if y_i * (np.dot(x_i, self.w) + self.b) <= 0:
                    self.w += self.learning_rate * y_i * x_i
                    self.b += self.learning_rate * y_i
                    misclassified += 1
            # 如果没有错误分类，提前结束训练
            if misclassified == 0:
                break
                
        return self
    
    def predict(self, X):
        return np.where(np.sign(np.dot(X, self.w) + self.b) == -1, 0, 1)
    
    def score(self, X, y):
        y_pred = self.predict(X)
        return np.mean(y_pred == y)
    
    # 获取用于绘制决策边界的参数
    def decision_boundary(self):
        return self.w, self.b

# 创建并训练感知机模型
perceptron = Perceptron(learning_rate=0.01, max_iterations=1000)
perceptron.fit(X, y)

# 评估模型
accuracy = perceptron.score(X, y)
print(f"Accuracy: {accuracy:.4f}")

# 绘制决策边界
w, b = perceptron.decision_boundary()
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
                     np.arange(y_min, y_max, 0.1))
Z = np.sign(np.dot(np.c_[xx.ravel(), yy.ravel()], w) + b).reshape(xx.shape)

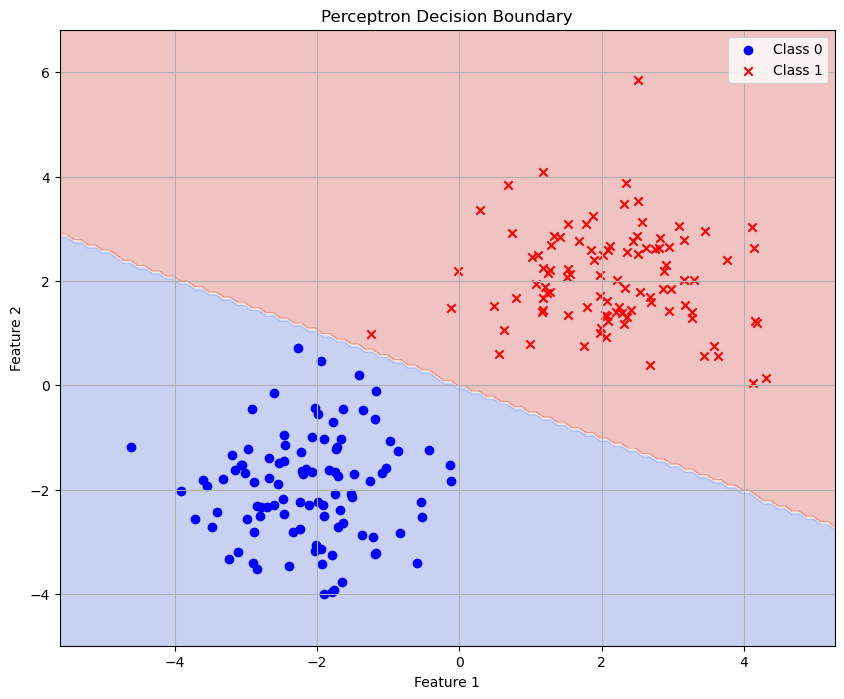
plt.figure(figsize=(10, 8))
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.coolwarm)
plt.scatter(X_neg[:, 0], X_neg[:, 1], c='blue', marker='o', label='Class 0')
plt.scatter(X_pos[:, 0], X_pos[:, 1], c='red', marker='x', label='Class 1')
plt.title('Perceptron Decision Boundary')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.grid(True)
plt.show()
PYTHON