K邻近法
1. 概述
kNN是一种基本分类与回归方法,这里讨论分类问题的KNN方法。kNN假设给定一个训练数据集,其中的实例类别已定。分类时,对新的实例,根据其 $k$ 个最近邻的训练实例的类别,通过多数表决等方式进行预测。kNN利用训练数据集对特征向量空间进行划分,并作为其分类的”模型”。三个基本要素是k值的选择、距离度量以及分类决策规则。
2. k邻近算法(简洁版)
2.1算法
(1)根据给定的距离度量,在训练集T中找出与 $x_i$ 最近邻的 $k$ 个点,涵盖这 $k$ 个点的邻域记作 $N_k(x)$.
(2)在 $N_k(x)$中根据分类决策规则(如多数表决)决定 $x$ 的类别 $y$:
$$y = \arg \max_{c_j} \sum_{x_i \in N_k(x)} I(y_i = c_j), \quad i = 1, 2, \dots, N; \quad j = 1, 2, \dots, K$$
其中,$I$ 为指示函数。
k近邻法的特殊情况是$k$ =1的情形,称为最近邻算法。
没有显式的学习过程。
2.2模型
当训练集、距离度量、$k$ 值及分类决策规则确定后,对于一个新的输入实例,它所属的类唯一地确定。特征空间中,对于每个训练点 $x_i$,距离该点比其他点更近的所有点组成一个区域,叫做单元;每个训练实例点拥有一个单元,所有训练实例点的单元构成对特征空间的一个划分。最邻近法将实例 $x_i$ 的类 $y_i$ 作为其单元中所有点的类标记。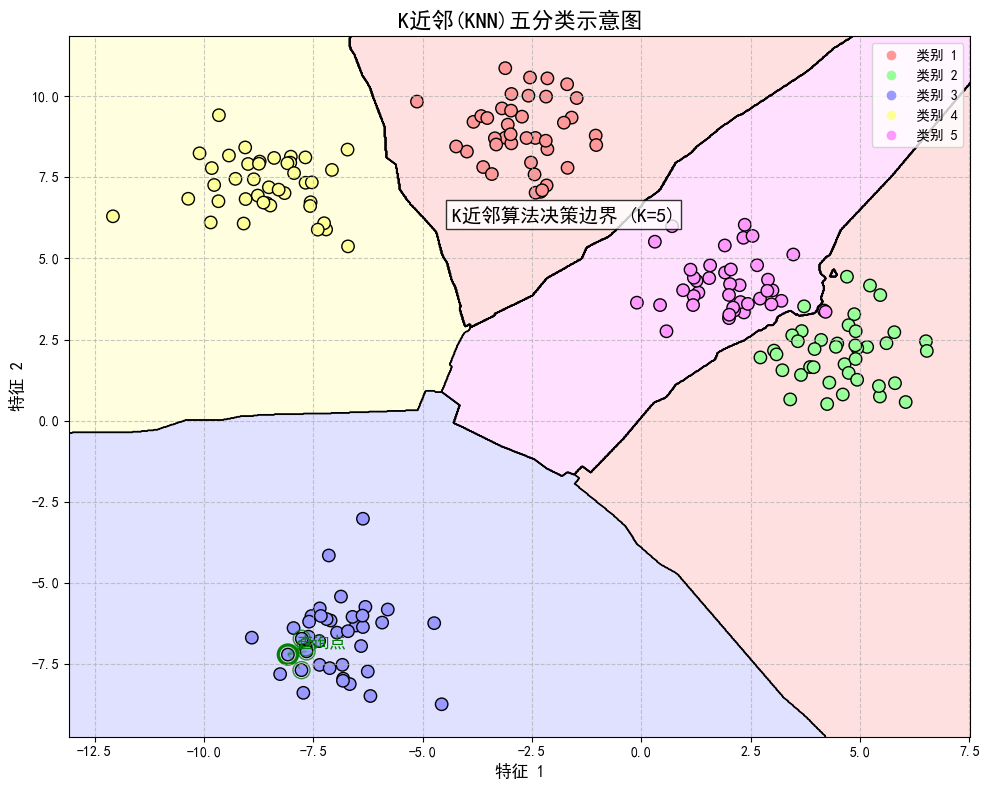
a)距离度量
特征空间中两个实例点的距离是两个实例点相似程度的反映。kNN模型的特征空间一般是n维实数向量空间$R^n$。使用的距离是欧氏距离,也可以是其它距离。
b)k值的选择
k值的选择会对k近邻法的结果产生重大影响。
如果选择较小的 $k$ 值,就相当于用较小的邻域中的训练实例进行预测,”学习”的近似误差(approximation error)会减小,只有与输入实例较近的(相似的)训练实例才会对预测结果起作用。但缺点是”学习”的估计误差(estimation error)会增大,预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声,预测就会出错。换句话说, $k$ 值的减小就意味着整体模型变得复杂,容易发生过拟合。
如果选择较大的 $k$ 值,就相当于用较大邻域中的训练实例进行预测。其优点是可以减少学习的估计误差。但缺点是学习的近似误差会增大。这时与输入实例较远的(不相似的)训练实例也会对预测起作用,使预测发生错误。k值的增大就意味着整体的模型变得简单。
如果 $k=N$,那么无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类。这时,模型过于简单,完全忽略训练实例中的大量有用信息,是不可取的。
在应用中,k值一般取一个比较小的数值。通常采用交叉验证法来选取最优的k值。
c)分类决策规则
$k$ 近邻法中的分类决策规则往往是多数表决,即由输入实例的 $k$ 个邻近的训练实例中的多数类决定输入实例的类。
多数表决规则(majority voting rule)有如下解释:如果分类的损失函数为 0-1 损失函数,分类函数为
$$f : \mathbb{R}^n \to {c_1, c_2, \cdots, c_K}$$
那么误分类的概率是
$$P(Y \neq f(X)) = 1 - P(Y = f(X))$$
对给定的实例 $x \in \mathcal{X}$,其最近邻的 $k$ 个训练实例点构成集合 $N_k(x)$。如果涵盖 $N_k(x)$ 的区域的类别是 $c_j$,那么误分类率是
$$\frac{1}{k} \sum_{x_i \in N_k(x)} I(y_i \neq c_j) = 1 - \frac{1}{k} \sum_{x_i \in N_k(x)} I(y_i = c_j)$$
要使误分类率最小即经验风险最小,就要使
$$\sum_{x_i \in N_k(x)} I(y_i = c_j)$$
最大,所以多数表决规则等价于经验风险最小化。
3. kNN的实现:kd树
3.1 kd树介绍
kd树(k-dimensional tree)是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是二叉树,表示对k维空间的一个划分,其每个结点对应于k维空间划分中的一个超矩形区域。
kd树的构造目的是实现高效的最近邻搜索,特别是在k维空间中的数据点很多时,直接计算距离的方法效率低下。
3.2 kd树的构造
kd树的构造过程是一个递归的过程:
- 在k维空间中选择一个坐标轴j进行切分(通常按轮流选择的规则)
- 在选定的坐标轴上,选择切分点,将数据集划分为两部分
- 对划分的两部分分别递归构建左右子树
常用的切分方式是选择当前维度上的中位数作为切分点,这样可以保证构造出的kd树是平衡的。
构造算法的数学描述如下:
$$\text{BuildKdTree}(P, depth):$$
$$
\begin{cases}
\text{如果 } P \text{ 为空,返回 } \text{null}\
\text{axis} = \text{depth} \bmod k\
\text{按 } \text{axis} \text{ 维度对 } P \text{ 中的点排序}\
\text{median} = \text{在 } \text{axis} \text{ 维度上的中位数点}\
\text{将 } \text{median} \text{ 作为根节点}\
\text{root.left} = \text{BuildKdTree}(P_{\text{left}}, \text{depth}+1)\
\text{root.right} = \text{BuildKdTree}(P_{\text{right}}, \text{depth}+1)\
\text{返回 } \text{root}
\end{cases}
$$
其中,$P_{\text{left}}$ 是 $\text{axis}$ 维度上小于 $\text{median}$ 的点集,$P_{\text{right}}$ 是大于 $\text{median}$ 的点集。
3.3 kd树的最近邻搜索
kd树最核心的操作是搜索给定点的最近邻。算法步骤如下:
- 从根节点开始,递归地向下遍历树
- 在每个节点,将目标点与当前节点比较
- 根据比较结果选择一个子树优先遍历
- 回溯时检查另一子树是否可能包含更近的点
- 如果可能,遍历另一子树
最近邻搜索的数学表达为:
$$\text{NearestNeighbor}(\text{node}, \text{target}, \text{best}):$$
$$
\begin{cases}
\text{如果 } \text{node} \text{ 为空,返回 } \text{best}\
d = \text{Distance}(\text{target}, \text{node.point})\
\text{如果 } d < \text{Distance}(\text{target}, \text{best}) \text{ 则 } \text{best} = \text{node.point}\
\text{axis} = \text{node} \text{ 的划分维度}\
\text{如果 } \text{target}[\text{axis}] < \text{node.point}[\text{axis}]\
\quad \text{first} = \text{node.left}\
\quad \text{second} = \text{node.right}\
\text{否则}\
\quad \text{first} = \text{node.right}\
\quad \text{second} = \text{node.left}\
\text{best} = \text{NearestNeighbor}(\text{first}, \text{target}, \text{best})\
\text{如果 } |\text{target}[\text{axis}] - \text{node.point}[\text{axis}]| < \text{Distance}(\text{target}, \text{best})\
\quad \text{best} = \text{NearestNeighbor}(\text{second}, \text{target}, \text{best})\
\text{返回 } \text{best}
\end{cases}
$$
3.4 kd树的复杂度分析
- 构建kd树的时间复杂度:$O(n\log n)$,其中$n$是数据点的数量
- 平衡kd树的空间复杂度:$O(n)$
- 最近邻搜索的平均时间复杂度:$O(\log n)$
- 最近邻搜索的最坏情况时间复杂度:$O(n)$(当数据分布极不均匀时)
kd树在低维空间(通常 $k<20$ )中表现良好,但在高维空间中由于”维度灾难”问题,其效率会急剧下降。在高维情况下,可能需要考虑其他数据结构如哈希或近似最近邻算法。